Ce sont: 

 

  l'hexaèdre (cube) 

 

 le tétraèdre

 

l'octaèdre

 
l'icosaèdre

 

le dodécaèdre

Pourquoi cinq seulement? Un pythagoricien ne pouvait en être surpris. Si limite il y a, cette limite ne peut être que Cinq.

Les cinq corps platoniciens sont les seuls polyèdres qui possèdent les caractéristiques suivantes:
* toutes leurs arêtes sont égales;
* toutes leurs faces ont la même surface;
* tous leurs angles sont égaux;
* ils s'inscrivent parfaitement dans une sphère et dans un cube.  

Ils sont par conséquent parfaits. C'est ainsi que les Platoniciens sont amenés à placer la théorie des polyèdres réguliers au faîte de la Géométrie, comme étant le couronnement de cette science.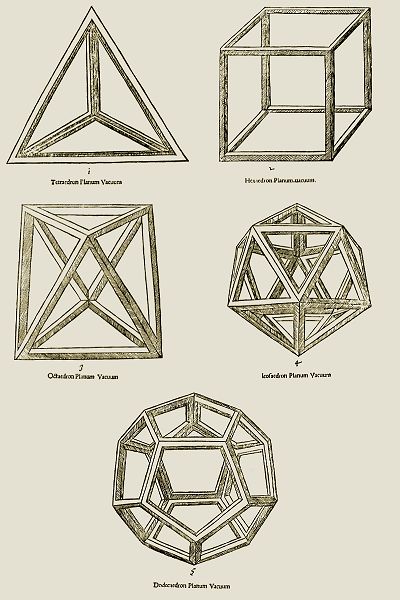

Le tétraèdre constitue la pyramide à la fois la plus simple et la plus harmonieuse: ses quatre faces sont des triangles équilatéraux, à côtés tous trois égaux à eux-mêmes.

Le dodécaèdre est le plus puissant des cinq polyèdres parfaits de la géométrie sacrée. Le dodécaèdre émet des ondes de forme de la quatrième dimension qui est un espace au-delà de la dualité, du bien et du mal, du conflit et du jugement.

Toutes les formes émettent des vibrations qu'on appelle ondes de formes. La différence avec les solides de Platon et la sphère est que leurs formes étant parfaitement symétriques, leurs vibrations le sont aussi.

C'est Pythagore qui fit le lien entre l'aspect Divin, les mathématiques et les formes géométriques. Pour Pythagore, nombre et harmonie expliquent l'ensemble du cosmos dans sa manifestation.