This is the standard order of writing reactions.  On the left side go the starting substances, or reactants, and on the right side go the substances that form in the reaction, which are the products.  In between the reactant and product sides goes the "yield sign" which is the familiar arrow  –––�?gt;.

Besides the normal yield sign, there are other arrows used in writing reactions, but these have different meanings:

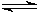
    This is the equilibrium double arrow for reversible reactions.

    This is the resonance arrow which is used to indicate the different resonance structures of a substance.

 

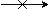
  This means "does not yield" in case you need to make the point!

Other information may be placed above or below the yield sign to save space.  For example,

   means "yields with heating" (temperature not specified).

 25°C
––––�?gt;    means "yields" at 25 degrees Celsius.

–––––�?gt;  means "yields in the presence of sulfuric acid."
H₂SO₄

–––––�?gt;  means "yields at 25 atmospheres pressure."
25 atm

 

 

 

More information that is given in a properly written reaction are the physical states of the reactants and products.  These are specified by the following abbreviations after the formulas:

(s)    means "solid"
(l)     means "liquid"
(g)    means "gas"
(aq)  means "aqueous solution" or "dissolved in water"

Thus H₂O (s) is water in the solid state (ice), H₂O (l) is water in the liquid state, and H₂O (g) is gaseous water vapor.

 

 

 

It is convenient to be familiar with about five "standard" types of reactions which are very common.  Recognizing the reaction type enables us to be able to predict the outcome of the reaction if we do not initially know what the products are.  The five types are

1.  Combination (or "composition" or "synthesis").  Two reactants combine to form a single product.
     A  +  B   ––�?gt;   C

Examples
2 Mg (s)  +  O₂ (g)   ––�?gt;   2 MgO (s)
CO₂ (aq)  +  H₂O (l)  ––�?gt;   H₂CO₃ (aq)

 

2.  Decomposition.  A single reactant breaks down to give two or more products.
     A   ––�?gt;   B  +  C

Examples
CaCO₃ (s)    CaO (s)  +  CO₂ (g)
H₂CO₃ (aq)   ––––�?gt;   CO₂ (g)  +  H₂O (l)

2 KClO₃ (s)     2 KCl (s)  +  3 O₂ (g)
                     MnO₂

 

3.  Single Displacement (or single replacement).  An element displaces another element from a compound.
     A  +  BX   ––�?gt;   B  +  AX    Element A must be "more active" than element B

Examples
Zn (s)  +  CuSO₄ (aq)   ––�?gt;   Cu (s)  +  ZnSO₄ (aq)
Ni (s)  +  2 HCl (aq)   ––�?gt;   H₂ (g)  +  NiCl₂ (aq)

4.  Double Displacement (or "metathesis").  Usually in ionic reactions, ions "exchange partners."
     AX  +  BY   ––�?gt;   BX  +  AY

Examples
AgNO₃ (aq)  +  NaCl (aq)   ––�?gt;   NaNO₃ (aq)  +  AgCl (s)
Pb(NO₃)₂ (aq)  +  2 KI (aq)   ––�?gt;   2 KNO₃ (aq)  +  PbI₂ (s)
HCl (aq)  +  NaOH (aq)   ––�?gt;   NaCl (aq)  +  H₂O (l)

We need to be familiar with the solubility rules of common ionic compounds in order to write the ionic and net ionic reactions.  In aqueous solution, soluble ionic compounds are completely separated into their positive and negative ions.  "Pb(NO₃)₂ (aq)" would be written "Pb²⁺ (aq)  +  2 NO₃^{�?/SUP> (aq)".  The formulas of insoluble ionic solids and weak and non-electrolytes are not separated like this because that does not happen in these cases.}

Formula equation:
Pb(NO₃)₂ (aq)  +  2 KI (aq)   ––�?gt;   2 KNO₃ (aq)  +  PbI₂ (s)

Ionic equation:
Pb²⁺ (aq)  +  2 NO₃^{�?/SUP> (aq)  +  2 K+ (aq)  +  2 I�?/SUP> (aq)   ––�?gt;   2 K+ (aq)  +  2 NO₃�?/SUP> (aq)  +  PbI₂ (s)}

"Canceling" the soluble "spectator ions" that appear on both sides gives the net ionic equation:
Pb²⁺ (aq)  +  2  I^{�?/SUP> (aq)   ––�?gt;   PbI₂ (s)}

Note that ionic and net ionic equations can be written for single displacement reactions as well.

 

5.  Combustion of a hydrocarbon in an oxygen atmosphere.
     Complete combustion gives carbon dioxide and water as the only products.

Examples
CH₄ (g)  +  2 O₂ (g)   ––�?gt;   CO₂ (g)  +  2 H₂O (g)
2 C₄H₁₀ (g)  +  13 O₂ (g)   ––�?gt;   8 CO₂  +  10 H₂O (g)

Balance the carbons first, then the hydrogens, and lastly the oxygens.  The coefficient in front of O₂ may be a fraction, such as 13/2.  In that case, multiply all the coefficients through by two so that you have the simplest whole-number coefficients.

 

 

 

When we balance chemical reactions, we want to have the same number of atoms of each element on each side of the equation.  If we have eight carbons on the left, we should have a total of eight carbons on the right, and so on.  Normally this is a trial and error process, although complex reactions can be very difficult to balance this way.  For such reactions, an algebraic approach can be incorporated into a computer program which will balance the reaction for you.  There are several such "equation balancers" on the Internet to use for free or purchase.  But most of the time, the reactions in your textbook can be balanced by the trial and error method.

Number One Rule in balancing reactions:  First, before balancing, be sure the formulas of the substances are written correctly!  Watch out for mistakes like "Na₂Cl₂" and "K₂(NO₃)₂."  The correct formulas are NaCl and KNO₃.  If you need two of them, use coefficients, don't change a correct formula:  2 NaCl and 2 KNO₃.  Check the charges of the ions from a table if necessary, to avoid writing things like "NaSO₄" when it should be Na₂SO₄.

When working problems based on a chemical equation (stoichiometry problems), it is very important that the reaction be balanced correctly, or the results of the calculations will almost certainly be wrong.

Reactions involving ionic substances are usually easier to balance than they may first appear.  Look at the following unbalanced reaction, for example:

Ca(NO₃)₂ (aq)  +  Na₃PO₄ (aq)   ––�?gt;   NaNO₃ (aq)  +  Ca₃(PO₄)₂ (s)

Rather than counting the oxygens individually, just balance the ions, NO₃^{�?/SUP> and PO₄3�?/SUP>.  Since there are two nitrates on the left, we need two nitrates on the right:}

Ca(NO₃)₂ (aq)  +  Na₃PO₄ (aq)   ––�?gt;   2 NaNO₃ (aq)  +  Ca₃(PO₄)₂ (s)

Since there are two phosphates on the right, we need two phosphates on the left:

Ca(NO₃)₂ (aq)  +  2 Na₃PO₄ (aq)   ––�?gt;   2 NaNO₃ (aq)  +  Ca₃(PO₄)₂ (s)

Now for the calciums.  There are three Ca on the right, so we need three on the left.  But that will unbalance the nitrates.  So after putting a coefficient of 3 in front of Ca(NO₃)₂, we will need to multiply the coefficient in front of NaNO₃ by three also, making it 6.

3 Ca(NO₃)₂ (aq)  +  2 Na₃PO₄ (aq)   ––�?gt;   6 NaNO₃ (aq)  +  Ca₃(PO₄)₂ (s)

And that does it.  Part method and part luck!