|
|
 |
|
Reply
| |
1. 50mL of 100mM lactic acid and 100mL of 100mM sodium lactate are mixed together to give a buffer. the pKa of lactic acid is 3.86. a.what is the pH of the buffer, and what is its concentration? b.is it a good buffer? why or why not? c. The pHis brought to 3.86 by adding strong acid or base, with negligible change in the total volume. What are the final concentrations of lactic acid and lactate ion? 2.Calculate Ka and pKa for a weak acid in aqueous solution, where [HA]=100mM and [H+]=[A-]=500 micrometers. 3. For the amino acids aspartic acid and histidine: a. go through the stepwise ionization, indicating, indicating (structural formulae) the forms present at each step and the net charge on each form. b. draw the corresponding titration curves, labelling the pKa's and the isoelectric points. 4. 4.92g of sodium acetate (MW=82D) is dissolved in water, the pH is adjusted to 4.2 with HCl, and the final volume is brought to 400mL with water. The pKa of acetic acid is 4.76. a.what are the concentrations of acetic acid and acetate ion in the final solution? b. is the solution a good buffer? why or why not? kenny. |
|
 First
Previous
2-15 of 15
Next
Last
|
Reply
| | (1 recommendation so far) | Message 2 of 15 in Discussion |
|
5. Starting with 75mM solutions of Na2HPo4 and NaH2PO4, explain how 700ml of a 75mM buffer, pH6.5, would be prepared. the pKa of the weak acid HPo4- is 6.86. 6. explain how 1L of a 200mM buffer, pH7.3, would be prepared from K2HPo4(MW=174D) and KH2PO4 (MW=136D). As in question 5, pKa=6.86 7. The weak base tris (hydroxymethyl) aminomethane( MW=121D), commonly called "Tris" is often used to prepare buffers. Its pKa is 8.3. Explain how 500mL of a 175mM buffer, pH8.7, could be prepared using Tris, if its conjugate acid form is not available. 8. 1.94g of histidine (MW=155.2D) is dissolved in water and the pH is brought to 6.5 with NaOH. The final volume is then brought to 250 ml with water. a.what forms of amino acid (see question 3) are present? b. what are the concentrations of each of these forms? c. Is the solution a good buffer? why or why not? |
|
Reply
| | From:  ·Steve· | Sent: 4/5/2008 8:52 PM |
That's a lot of problems!  I'll get you started with the first one: 1. a) For this one, you can simply use the Henderson-Hasselbalch equation:
pH = pKa + log (moles of sodium lactate / moles of lactic acid)
b) It looks OK. It is generally best to have near equal concentrations of weak acid and conjugate base in the buffer, so it can accommodate equally well the addition of either acid or base with changing pH too much. The concentration of lactic acid is half the concentration of sodium lactate, but there is still a significant amount of both present.
c) Here pH = pKa, so moles of sodium lactate = moles of lactic acid.
Initially, the moles of lactic acid = 0.0050 mol and the moles of sodium lactate = 0.010 mol. So, we need to add a strong acid such as HCl to bring down the moles of sodium lactate until it equals the moles of lactic acid. Let X = the moles of HCl added. Then,
moles of sodium lactate = 0.010 �?X
moles of lactic acid = 0.0050 + X
Setting the two term equal to each other,
0.010 �?X = 0.0050 + X
you can calculate X, the moles of HCl added, and then you can calculate the moles of sodium lactate and lactic acid. The moles of either one divided by the total volume in liters gives the molarity (will be the same for each).
I'll let you chew on the rest of these, and if you get stuck, show me what you did so I can see where you're "at.". It is also easier to take them one problem at a time.  Question 2: >> [H+]=[A-]=500 micrometers << That is supposed to be 500 micromolar, 500 μM, I presume.
Steve
|
|
Reply
| |
in question one u told me to use pKa + log(moles sodium lactate/moles lacyic acid) wouldnt that be 3.86+log (0.1M/0.1M) which give a pH of 3.86? and the second part which asks what is its conc., how do i detemine that? |
|
Reply
| | | From: ·Steve· | Sent: 4/6/2008 6:28 PM |
Moles = volume in liters X molarity, so moles of lactic acid = 0.050 L X 0.100 mol/L = 0.0050 mol, and moles of sodium lactate = 0.0100 L X 0.100 mol/L = 0.0100 mol. In the Henderson-Hasselbalch equation, the ratio in the last term is molarity of conjugate base over molarity of weak acid, which is molarity of lactate ion over molarity of lactic acid. The molarities are moles divided by the total volume, 150 mL or 0.150 L. The ratio of molarities is therefore moles of sodium lactate / 0.150 L = 0.0100 mol / 0.150 L = 0.0667 M = 2.0 moles of lactic acid / 0.150 L 0.0050 mol / 0.150 L 0.0333 M Note that these are not simply the initial molarities of the two substances before making the buffer solution, they are the molarities of the two substances in the buffer solution after they have been mixed together. (You can also use the dilution formula to calculate the molarities after mixing, M1V1 = M2V2.) However, since the volumes in the numerator and denominator are the same, they cancel, so the ratio is simply moles of sodium lactate = 0.0100 mol / 0.150 L = 0.0100 mol = 2.0 moles of lactic acid 0.0050 mol / 0.150 L 0.0050 mol Therefore, in the Henderson-Hasselbalch equation, you can simply use moles of the conjugate base and weak acid in the last term, which saves a little time.  But normally, we need to use molarities when working pH problems. pH itself is the minus log of the hydrogen ion concentration in moles per liter, not simply the minus log of the moles of hydrogen ion. So we have to keep on our toes, but sometimes it is convenient to use amounts in moles. Steve |
|
Reply
| |
can i get some help with question 3 and 4 please? |
|
Reply
| | | From: ·Steve· | Sent: 4/8/2008 7:13 AM |
Question 3 At the bottom of the following page, http://www.chem.usu.edu/~sbialkow/Classes/3600/Overheads/H3A/H3A.html, is the actual titration curve of aspartic acid. At different pHs, the carboxylic acid groups and the amino group will either be protonated or deprotonated. For example, at low pH, everything will be in protonated form, depending on the pKa value for the group. For the carboxylic acid group, this is the neutral –COOH form, while for the amino group, the structure is –NH3+ with a charge of +1. The deprotonated form of a carboxylic acid group is –COO�?/SUP> with a charge or �?. The deprotonated form of the ammonium ion group, –NH3+, is the amino group –NH2 which is neutral (charge = 0).
For aspartic acid, the pKa values are 1.990, 3.900, and 10.002. The first two are carboxylic acid protons and the last is the ammonium proton (from the above website).
With the Henderson-Hasselbalch equation you can calculate the ratio of the deprotonated group (conjugate base form) and the protonated group (weak acid form). Above about one pH unit above or below the pKa, the group is essentially in one form, with only a small percentage in the other. When pH = pKa, there is a 50/50 mixture of both forms.
So, referring to the Ka values, below a pH of about 1, all three groups will be in their protonated form and the overall charge will be 0 + 0 + (+1) = +1.
At a pH of about 2, the first carboxylic acid group will be in its deprotonated form, –COO�?/SUP>, while the second one will still be –COOH and the amino group will also still be protonated as –NH3+. The overall charge will be �? + 0 + (+1) = 0.
At a pH of about 5 (between the Kas of the second carboxylic acid group and the ammonium ion group) both carboxylic acid groups will be in their –COO�?/SUP> form, but the ammonium ion group will still be in its –NH3+ form. Thus the overall charge at this pH is �? + (�?) + (+1) = �?.
Finally, at a pH of about 11 or higher, all three group will be in their deprotonated forms, –COO�?/SUP>, –COO�?/SUP>, and –NH2, with an overall charge of �? + (�?) + 0 = �?.
Steve
|
|
Reply
| | | From: ·Steve· | Sent: 4/8/2008 7:55 AM |
Question 4 First calculate the moles of sodium acetate. Next calculate the following ratio,
moles of sodium acetate / moles of acetic acid
at the desired pH of 4.2 using the Henderson-Hasselbalch equation:
4.2 = 4.76 + log (moles of sodium acetate / moles of acetic acid)
When you add HCl, you are converting acetate ion from sodium acetate to acetic acid and NaCl:
NaC2H3O2 (aq) + HCl (aq) ––�?gt; HC2H3O2 (aq) + NaCl (aq)
Initially: I 0 0 0
After Rxn: I �?x x x (x)
"I" is the initial moles of sodium acetate (from the 4.92 g).
Solve for x:
(I �?x) / x = ratio from the HH equation.
I �?x will be the moles of sodium acetate in the solution and x will be the moles of acetic acid in the solution. Divide each by the total volume, 0.400 L, to get their molarities.
Steve
|
|
Reply
| | | From: ·Steve· | Sent: 4/8/2008 1:57 PM |
Oops, correction, I wrote the "x" wrong for the moles of HCl in the reaction. It should be NaC2H3O2 (aq) + HCl (aq) ––�?gt; HC2H3O2 (aq) + NaCl (aq)
Initially: I x 0 0
After Rxn: I �?x 0 x (x)
The moles of HCl added is "x" initially here, and since it should be the limiting reactant, there will not be any HCl remaining after it reacts with the sodium acetate. The moles of acetic acid formed will equal the moles of HCl reacted, which is also x. The calculations are still the same as before, where you solve for x and calculate the molarities.
Steve |
|
Reply
| |
thanks steve you have been very helpful and also efficient thus far! the assignment is due for this thursday and i am a bit pondering on question 7 now ..help please! and also a and b of question 8. thanks again in advance |
|
Reply
| | | From: ·Steve· | Sent: 4/9/2008 11:08 PM |
I'll look at these after class tonight. All of these problems are rather complicated, with lots of details to understand! Steve |
|
Reply
| | | From: ·Steve· | Sent: 4/10/2008 2:36 AM |
Question 7
You can prepare the conjugate acid form by adding HCl.
First, calculate the ratio moles of tris / moles of Htris+ that gives a pH of 8.7 using the Henderson-Hasselbalch equation.
Then the problem is much like Question 4.
total moles of tris = (0.500 L)(0.175 mol/L) = 0.0875 mol (This is the total moles of tris plus its conjugate acid.)
tris (aq) + HCl (aq) ––�?gt; Htris+Cl�?/SUP> (aq)
Initially: 0.0875 mol x 0
After Rxn: 0.0875 �?x 0 x
(0.0875 �?x) / x = ratio of moles of tris / moles of Htris+ from HH.
Solve for x, the moles of HCl to be added. Dilute to a final volume of 500 mL.
|
|
Reply
| | | From: ·Steve· | Sent: 4/10/2008 6:13 AM |
Question 8
I think that HCl rather than NaOH will have to be added to the solution of histidine to bring the pH down to 6.5. The initial pH of a solution of histidine (a basic amino acid) should be greater than 7 initially, so adding NaOH would just make the pH too high.
I'll link right to the graphic:
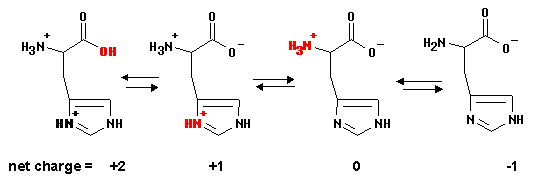
My labels –�?gt; H3A2+ H2A+ HA A�?/SUP>
It gives pKa1 = 2.3 (COOH), pKa2 = 6.0 (imidazole ring NH+), and pKa3 = 9.6 (amino NH3+)
Another site gives 1.78, 5.97, and 8.97 and similar (values are not reported consistently on the Internet).
The order is most acidic to least acidic group. Therefore the amino NH2 group is the most basic.
At pH 6.5, the COOH group is essentially 100% COO�?/SUP> and the amino group is essentially 100% NH3+. Since the pH of 6.5 is near the second pKa for the imidazole ring NH+ group, there will be a mixture of NH+ (conjugate acid) and N (conjugate base) forms for this group. So it's this pKa you need to use in your calculations.
Now it's the same process as in the other problems:
1. Calculate the moles of histidine from the given number of grams. This will be the total moles of the weak base + conjugate acid form. Below, I am calling the moles of histidine "I".
2. Use HH to calculate the ratio of moles of HA / H2A+.
3. Adding the NaOH. If we are starting with histidine in its charge = 0 zwitterion form, it should form a basic solution with a pH greater than 7. In that case we would have to add HCl instead of NaOH to bring the pH down to 6.5. According to http://alpha.chem.umb.edu/chemistry/ch313/Exp5%20hist.pdf, the pH of a 0.1 M solution of histidine is 7.8. If we started with the hydrochloride salt of histidine, H2A+Cl�?/SUP> by my labeling, then the initial pH would be low and NaOH would be needed to bring up the pH. But the given molecular weight is for neutral histidine, not its hydrochloride.
Here's the now familiar reaction pattern with the initial number of moles, same as in the other problems:
HA (aq) + HCl (aq) ––�?gt; H2A+Cl�?/SUP> (aq)
Initially: I x 0
After Rxn: I �?x 0 x
Like before, solve for x: (I �?x) / x = ratio from the HH equation. Divide the moles of HA and H2A+ by the total volume (0.250 L) to get their molarities.
And that should do it! 
Steve |
|
|
First
Previous
2-15 of 15
Next
Last
|
|
|
Free Forum Hosting
Important Announcement
Return to General