 |
Reply
 | | From:   N_2006 (Original Message) N_2006 (Original Message) | Sent: 4/11/2008 10:59 PM |
Cadium metal is added to 0.350 L of an aqueous solution in which [Cr^3+] = 1.00 M What are the concentrations of the different ionic species at equilibrium? Chem Equation: 2 Cr^3+ (aq) + Cd (s) <--> 2 Cr^2+ (aq) + Cd^2+ (aq) Kc = 0.288 Answer: So I set up an ICE chart 2 Cr^3+ (aq) + Cd (s) <--> 2 Cr^2+ (aq) + Cd^2+ (aq) I 1.00 M C -2x M + 2x + x E (1.00 - x) M 2x x Then sub that into the Kc equation: 0.288 = (2x)^2 (x) divided by (1.00 - 2x)^2 So now I don't know how to solve for x. I cannot use the quadractic formula.
Thanks for your help!
|
|
 First First
 Previous
2-8 of 8
Next Previous
2-8 of 8
Next Last
Last
|
Reply
 | | From:   ·Steve· ·Steve· | Sent: 4/12/2008 12:44 AM |
Don't forget the "2" in the "1 �?2x" term! 2 Cr3+ (aq) + Cd (s) 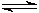 2 Cr2+ (aq) + Cd2+ (aq) 2 Cr2+ (aq) + Cd2+ (aq)
I 1.00 M �?nbsp; 0 0
C �?x �?nbsp; +2x +x
E 1.00 �?2x �?nbsp; 2x x Yep, you will have to solve a cubic equation to get x here! 
0.288 = (2x)2(x) = 4x3
(1 �?2x)2 4x2 �?4x + 1
Get this in the form ax3 + bx2 + cx + d = 0.
Then you can use the cubic formula to calculate the roots, or more easily, use one of cubic calculators on the Internet:
Good problem!
Steve |
|
Reply
 | | From:   N_2006 N_2006 | Sent: 4/12/2008 6:35 PM |
Awesome.. I never thought of that! I have an exam this tuesday and I need to do well, but the questions are hard! Also someone said that I could use the 5% rule and cancel out the x? Do you know what that is?
Thanks Steve!
|
|
Reply
 | | From:   ·Steve· ·Steve· | Sent: 4/13/2008 7:47 AM |
When x is very small compared to the initial value, then we can reasonably assume in the calculation that terms such as "I �?x" or "I �?2x" are approximately equal to I, where "I" is an initial concentration. The 5% rule says that if the amount subtracted, such as x or 2x, is less than about 5% of the initial value, then using the approximation will not affect the calculated value of x if we round it to about two or three significant figures, which is typical. In this problem, one of the equilibrium terms is 1.00 �?2x. Plugging the equilibrium terms into the equilibrium constant expression gives, 0.288 = (2x)2(x)
(1.00 �?2x)2 Approximating that 1.00 �?2x �?1.00, we have, 0.288 = (2x)2(x)
(1.00)2 Or, 0.288 = 4x3, x = 0.416 M. Is this a valid answer? We'll test it with the 5% rule. To pass the 5% rule, 2x must be less than 5% of 1.00, since it was 2x, not just x, that was subtracted from the initial value of 1.00 M. Let's see: 2(0.416 M) X 100 = 83.2%  1.00 M Ouch! This percentage is much too high, so the approximation is invalid. Therefore, we have to calculate x much more accurately, which in this case, means solving a cubic equation for x without using the approximation. You will get three answers (roots), of which only one will either not be negative, or, will not give a negative concentration when inserted into 1.00 �?2x. All three solutions are valid mathematically, but physically, you cannot have negative concentrations. Steve |
|
Reply
 | | From:   ·Steve· ·Steve· | Sent: 4/13/2008 7:50 AM |
Good Luck on you exam!  |
|
Reply
 | | From:   ·Steve· ·Steve· | Sent: 4/13/2008 7:57 AM |
BTW, an exam question would likely not require you to solve a cubic equation, so if you have to, your instructor may expect you to use the 5% rule, possibly even if it is invalid to do so (when x or 2x or whatever is greater than 5% of the initial value). However, it is common to have to use the quadratic formula to solve quadratic equations for x. But again, you may be able to use the approximation, especially for weak acid and weak base equilibria. Steve |
|
Reply
 | | From:   ·Steve· ·Steve· | Sent: 4/13/2008 5:53 PM |
One more way I forgot to mention: the method of successive approximations. Here's how that works: 1. Start with the original equilibrium constant expression and solve for x using the approximation that the 1.00 �?2x term is 1.00: 0.288 = 4x3 x = 0.4160
(1.00 �?2(0))2 2. Now repeat the calculation, plugging x = 0.416 into the denominator term, and solve for x again: 0.288 = 4x3 x = 0.1267
(1.00 �?2(0.416))2 3. Keep repeating this process, plugging the previous value of x into the denominator and solving for x again. The next calculation is, 0.288 = 4x3 x = 0.3424
(1.00 �?2(0.1267))2 What will happen, if your initial value of x is not too far off, is convergence of x to a constant value. Although I have written rounded values of x here, I did not round x in the actual calculations. I just stored each value on my calculator and used the RCL button to recall it in the next iteration. I continued calculating x this way and got the following values: 0.1927 0.3007 0.2253 0.2790 0.2414 0.2681 0.2493 0.2626 0.2532 0.2598 0.2552 0.2585 0.2561 0.2578 0.2566 0.2574 0.2569 0.2573 So we can tell that x is about 0.257 M. When you plug this value of x back into the equilibrium constant expression, you get, 4(0.257)3 = 0.287
(1.00 �?2(0.257))2 This is almost the correct value of Kc. With a little trial and error, you can get another digit. Trying x = 0.2571 as a guess, I get Kc = 0.28804, closer to the correct value of Kc of 0.288, so this is a better value of x. Or, you could continue the above procedure and gradually improve you value of x that way.  It is probably faster to use the cubic formula, but if you don't have that, this is an alternate method that should work. A possible problem is, if your initial value of x is too far off, you might get convergence to one of the other roots of the equation instead of the physically valid one. But most of the time, this method will give the right answer. It is probably faster to use the cubic formula, but if you don't have that, this is an alternate method that should work. A possible problem is, if your initial value of x is too far off, you might get convergence to one of the other roots of the equation instead of the physically valid one. But most of the time, this method will give the right answer. Steve |
|
Reply
 | | From:   N_2006 N_2006 | Sent: 4/13/2008 11:33 PM |
Thanks Steve, Yeah we never went over using cubic equations for this chem class, only quadratic and the 5% rule. Most likely she will not expect us to have to use the cubic. |
|
 First First
 Previous
2-8 of 8
Next Previous
2-8 of 8
Next Last
Last
|
|
 Free Forum Hosting
Free Forum Hosting