It is due to Le Chatelier's principle, called the "common ion effect" here.
Take the equilibrium equation of solid PbCl2 in equilibrium with dissolved PbCl2 in aqueous solution:
PbCl2 (s)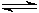 
Pb2+ (aq) + 2 Cl�?/SUP> (aq)
If you add more Cl�?/SUP> ion, the reverse (<–�? reaction will occur until the reaction is at equilibrium again. Therefore, some solid PbCl2 would precipitate out, leaving less dissolved in solution. Dissolving the PbCl2 in a solution that already has the Cl�?/SUP> ion in it initially gives the same result in terms of the equilibrium solubility of PbCl2.
Choices (b) and (c) are also solution which have chloride ion in them (0.1 M), but the CaCl2 solution would have twice the chloride ion, 0.2 M, since each CaCl2 gives 2 Cl�?/SUP> ions.
You can also calculate the molar solubilities and compare the values.
1. molar solubility of PbCl2 in pure water:
PbCl2 (s) 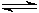Pb2+ (aq) + 2 Cl�?/SUP> (aq) Initially: �?nbsp; 0 0
At Equilib: �?nbsp; x 2x
Ksp = (x)(2x)2
x is the molar solubility of PbCl2 in pure water.
2. molar solubility of PbCl2 in a solution that is 0.1 M in chloride ion:
PbCl2 (s) 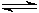Pb2+ (aq) + 2 Cl�?/SUP> (aq) Initially: �?nbsp; 0 0.1 M
At Equilib: �?nbsp; x 0.1 + 2x
Ksp = (x)(0.1 + 2x)2 �?(x)(0.1)2
x is the molar solubility of PbCl2, but will be less than the molar solubility in pure water.
3. If the chloride concentration is 0.2 M, then we would have,
Ksp = (x)(0.2 + 2x)2 �?(x)(0.2)2
x is the molar solubility of PbCl2, but will be less than the molar solubility in a solution that is 0.1 M chloride ion. As the concentration of Cl�?/SUP> ion goes up, the molar solubility of PbCl2 is seen to go down.
Steve
Free Forum Hosting
Important Announcement
Prev Message
