Ooops, reposting because I made a boo-boo with the mass of the water!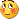 
Hi, Devin, I'll look at your calculations for unknown #1.
I gather that the unknown is a solid and it weighs 2 g (I'll go with 2.00 g). Since you could not use a balance, I assume that it was pre-weighed for the experiment. I also don't know why you are given the volume of the solid unknown, 1.30 mL, because we do not need that for the molecular weight calculations. It would not be accurate anyway if the solid is in particle or powder form with air taking up some of the volume. Same with the total volume of the solution, 11.62 mL. For the molecular weight calculation, we only need the mass of the solute, the mass of the solvent, and ΔTf.
>> Mass of water = 11.62 g <<
This is the volume of the solution (solvent + solute) which we don't need. The mass of the water alone is about 10.0 g since the density of water is about 1 g/ mL. If you had the temperature at which the volume of the water was measured, you could use a more exact density value and get a more accurate mass. For example, at 25°C, the mass would be 10.00 mL X 0.997044 g/mL = 9.970 g. (Earlier I divided instead of multiplying, wasn't watching my units!)
Your calculations of the molality and molecular weight are correct, except for the mass of the water.
Concerning the total volume of the solution, if you needed to determine the molarity of the solution, rather than the molality, you would need the total volume, 11.62 mL. If you needed to calculate the osmotic pressure of the solution, you would need the molarity for that. Other than for something like that, the total volume of the solution is not needed.
(a) They want to know specifically if the calculated MW will be too high or too low if all of the unknown does not dissolve. Hint: What will happen to ΔTf if less solute is dissolved in the solution? From that, tell what the effect would be on the MW.
(b) ΔTf is determined from the difference between the freezing point of the pure solvent and that of the solution. For #1, this was 0.00°C �?(�?.06°C) = 2.06°C. Try adding 0.63° to each value and taking the difference again. 
(c) That is right, the actual molality will be different from what you think it is. Will the molality really be higher or lower because of the extra water in the tube? In turn, what will this do to ΔTf, and in turn what will that do to your calculated MW?
Steve
Free Forum Hosting
Important Announcement
First 
0 recommendations 